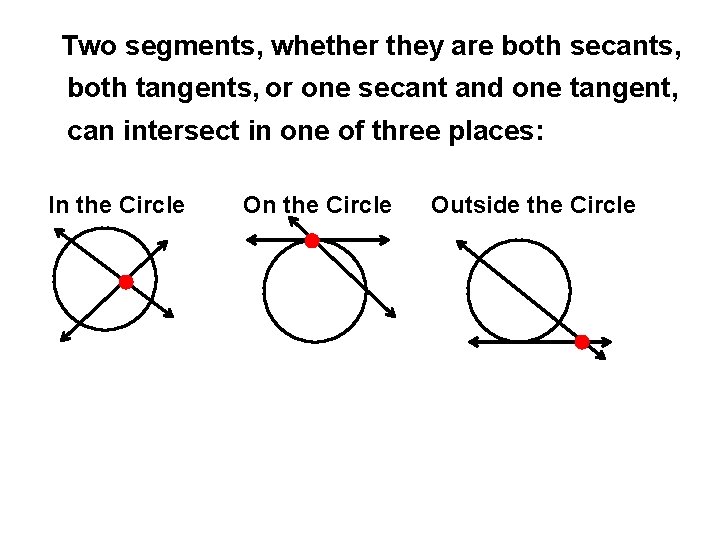
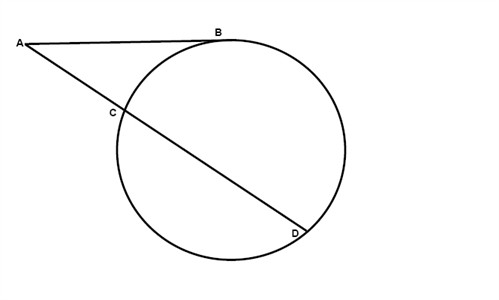
One secant and one tangent 104244-One secant and one tangent calculator

We go over how to integrate products of secants and tangents, as long as we either have an even number of secants or an odd number of tangentsTangent and Secant Transformations (pp 3 of 7) Precalculus HS Mathematics Unit 04 Lesson 02 The graph below shows one period of the tangent function, and labels some important features of the graph By hand, sketch each transformation of f (x) tan x , and tell how the location of each asymptote and point are affected = 2 4 , 1) 4 x 2 ©10, TESCCC b 1AsymptotesTangent and secant lines is greatest where the graph of f(x) is curved If the graph of y = f(x) is sharply curved, the value of Δx must be very close to 0 for the secant line to be close to the tangent line You may also have noticed that the difference between the slope of the secant and the slope of the tangent line was greater when the slope of the tangent line was large (and

Angle Of Intersecting Secants Theorem

One secant and one tangent calculator

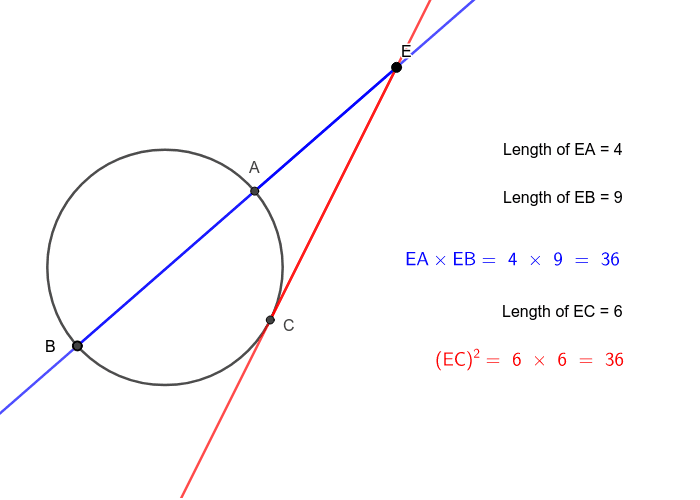
One secant and one tangent calculator-A secant line connects two points on a curve The slope of a secant line is the average rate of change between two points on a curve A tangent line touches one point The slope of a tangent line is the instantaneous rate of change at a single point on a curve The slope of a tangent line at a point is a derivative at that pointIt is called a secant line In Lesson 6, we saw that =tan(𝜃°), where ̅ lies on the line tangent to the unit circle at (1,0), which helped to explain how this trigonometric function got its name Let's introduce a new function sec(𝜃°),the secant of 𝜃, to be the length of ̅̅̅̅ since this segment is on the

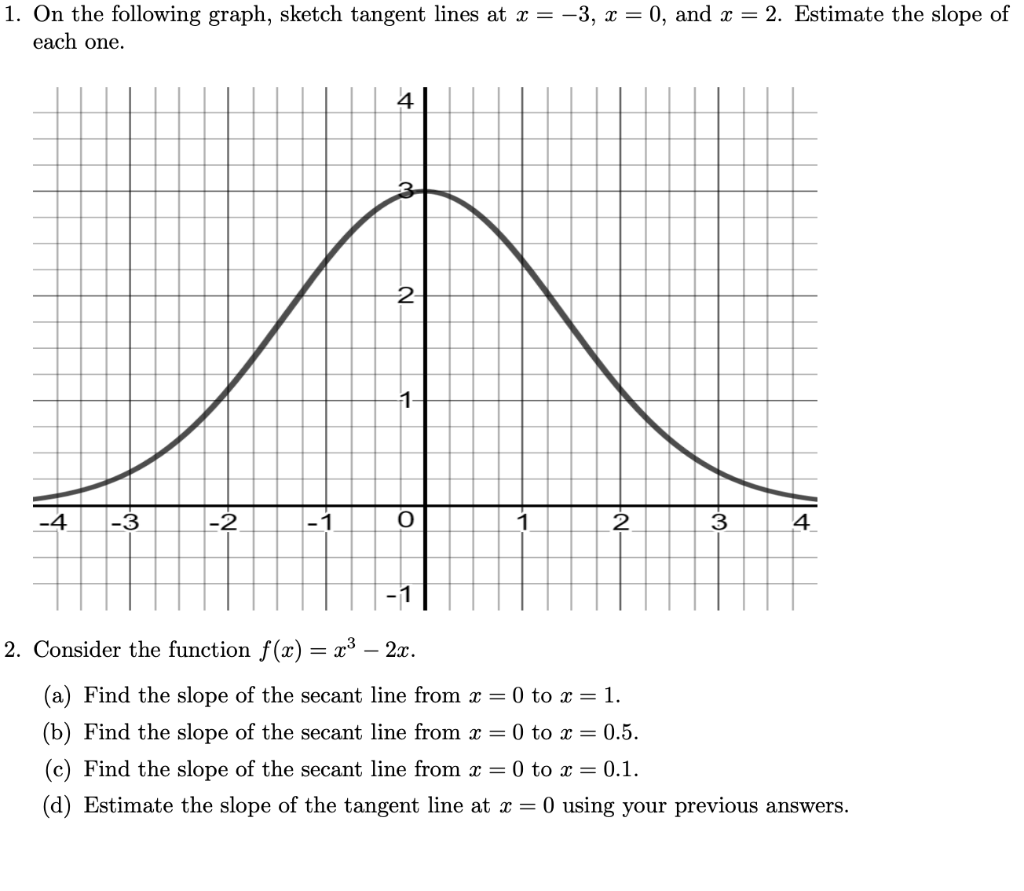
1 On The Following Graph Sketch Tangent Lines At X Chegg Com

Something as innocent looking as a simple relationship between slopes of tangent lines and areas of regions in the plane turns out to be one of the most transformative observations in the history of mathematics And was first noticed by Newton and Leibniz in the 17th century The idea behind the calculation we just did for y=x squared generalizes to any smooth curve y=f of x Choose someMATH 1371 Fall 10 Secant/Tangent Lines, Average/Instantaneous Velocity Jered Bright To do step one, we need to know the average velocity, and with this we need to know a second time value 3 When t =2, s(2)= 5(2)2 7(2)11 = 1411 =5 4 The first method mentioned in this step will be omitted and is left to the reader So we select our other time to be t =u and so s(u)=Definitions of Tangent, Secant, and Cosecant Let denote an angle Definition The tangent of , denoted is Definition The secant of , denoted is Definition The cosecant of , denoted is We summarize information about the domain and range of the six trig functions Domain equals Range equals 1,1 Domain equals Range equals 1,1

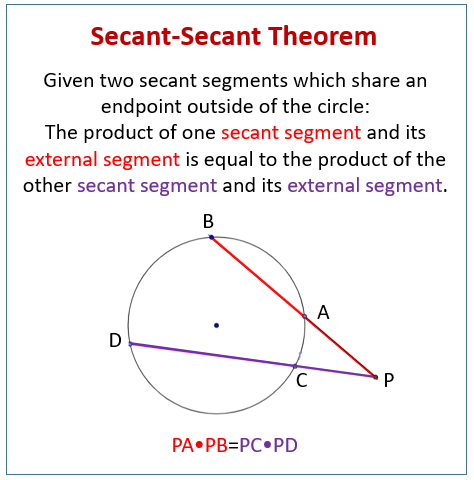
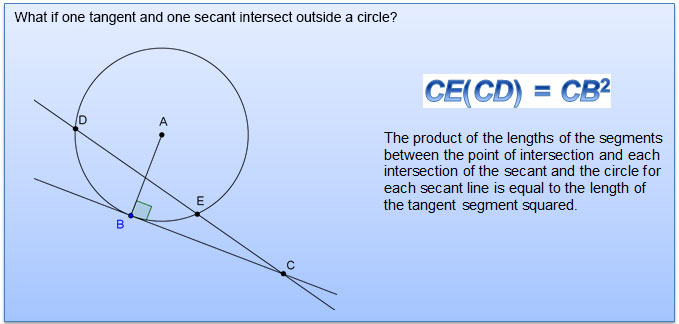
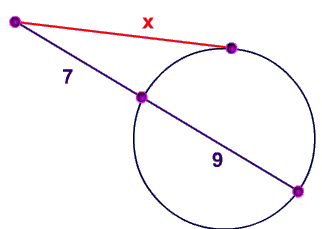
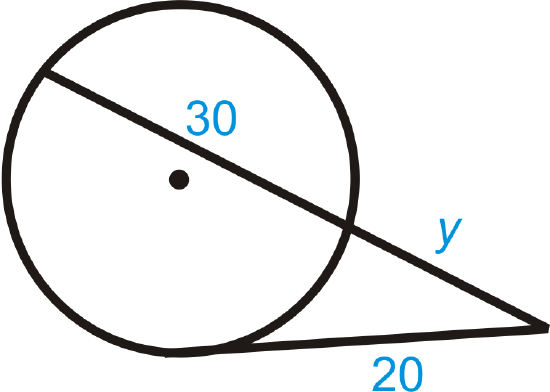
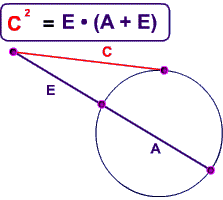
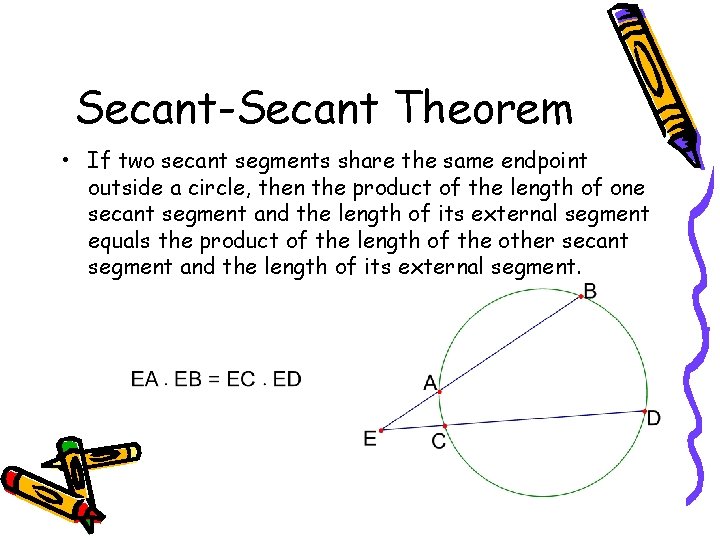
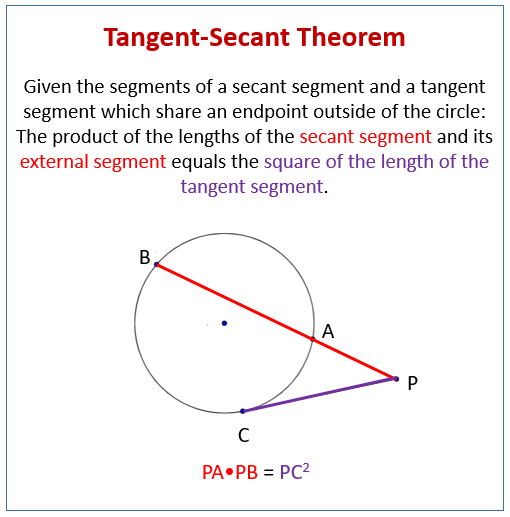
Live • Segments of Secants Theorem Two secant segments which share an endpoint outside of the circle The product of one secant segment and its external segment is equal to the product of the other secant segment and its external segment Errata For the example 2, the answer should be x = 9 Show Stepbystep SolutionsTrigonometric Integrals Involving Powers of Secant and Tangent Part 1Tangent and Secant Formula If a secant and a tangent of a circle are drawn from a point outside the circle, then the product of the lengths of the secant and its external segment equals the square of the length of the tangent segment

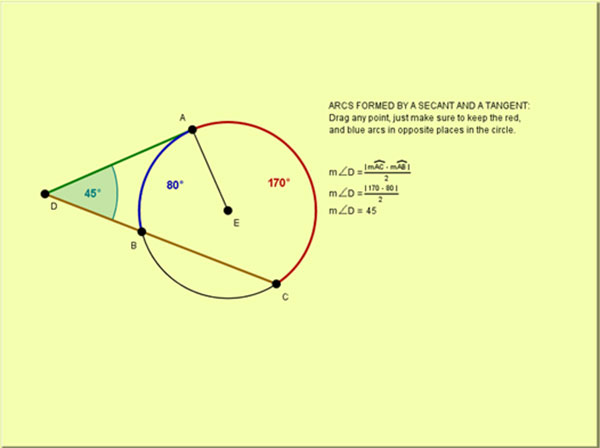
Onehalf the difference of the measures of the intercepted arcs whenever two secants intersect outside of a circle, a secant and a tangent intersect, or two tangent lines intersect TINspire™ Navigator™ System • Quick Poll • Screen Capture TINspire™ Technology Skills • Download a TINspire ;A segment of a tangent line with exactly one endpoint on the circle Secant — Tangent Theorem If a secant and a tangent intersect in the exterior of circle, then the product of the lengths of the secant segment and its external segment equals the length of the tangent segment squared c AC ø ßc Dc i EX 3 Find the value of x · As we explore trig identities and their graphs further, it is important to emphasize how each of them relate to one another When we look at any given right triangle, we know that sine = the opposite side (from a chosen angle) over the hypotenuse, which is the longest side Cosine = adjacent over hypotenuse, and tangent = opposite over adjacent

Tangent Secants Their Arcs And Angles Formula Pictures Interactive Demo And Practice Problems

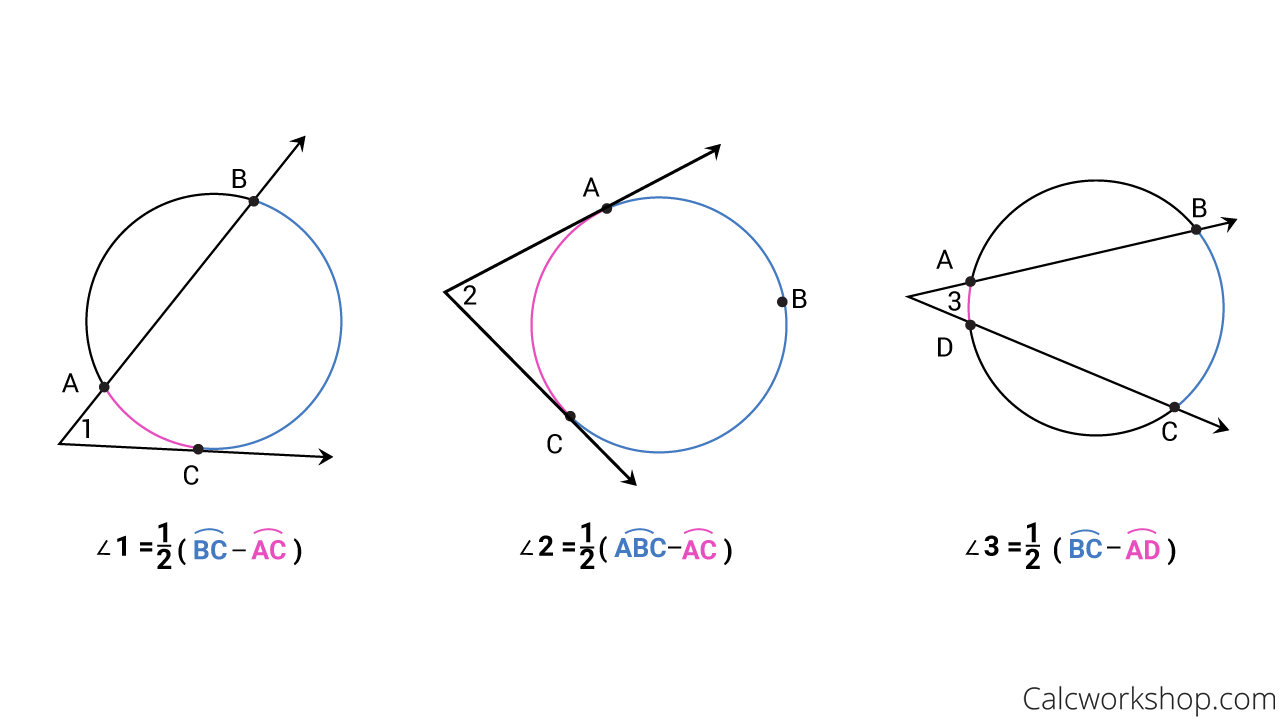
Intersecting Secants Theorem Explained W 15 Examples

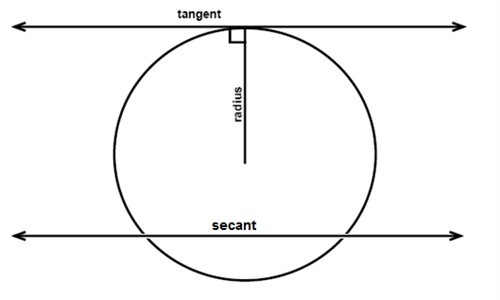
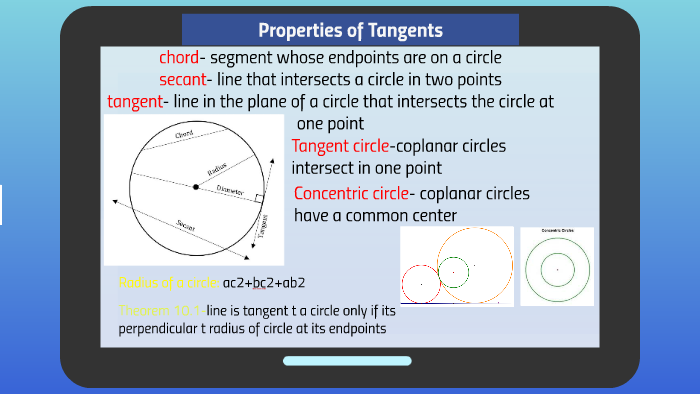
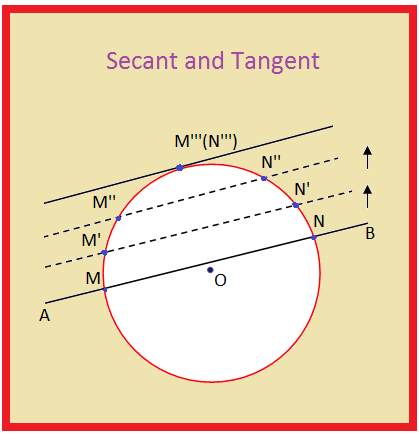
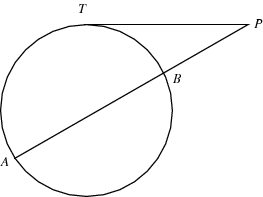
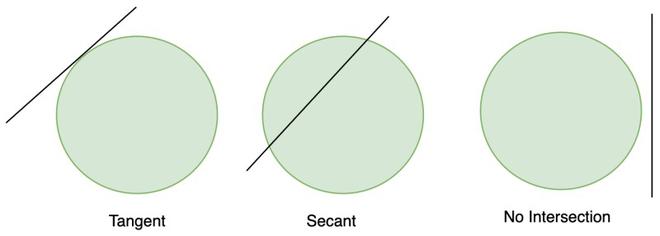
Except in this variation we have a tangent in the secant From point , we'll draw a tangent line, not a secant Then draw a second line which is a secant Still, we have a large arc which is and a smaller arc which is Same exact setup Same formula Except now, we don't have a missing arc in between One arc goes all the way to the point of the tangent line And the other arc starts atCosecant, Secant & Cotangent mcTYcosecseccot091 In this unit we explain what is meant by the three trigonometric ratios cosecant, secant and cotangent We see how they can appear in trigonometric identities and in the solution of trigonometrical equations Finally, we obtain graphs of the functions cosecθ, secθ and cotθ from knowledge of the related functions sinθ, cosθ and tanθA straight line which cuts a circle in two distinct points is called a secant to the circle In case (ii) above, AB is a secant to the given circle A straight line which touches a circle at only one point is called a tangent to the circle The point at which it touches

Plane And Solid Geometry Ex 670 If Two Chords Intersect Within A Circle Es Tablish A Proportionality Among The Segments Of The Chords Place The Product Of The Extremes Equal To The Product

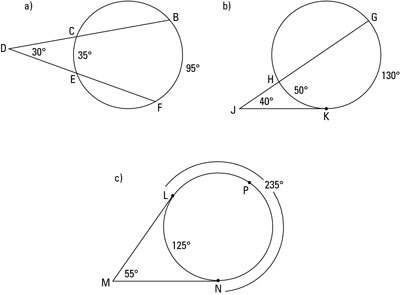
How To Determine The Measure Of An Angle Whose Vertex Is Outside A Circle Dummies

Therefore to find this angle (angle K in the examples below), all that you have to do is take the far intercepted arc and near the smaller intercepted arc and then divide that number by two!Circle Circle Theorem 1 Tangent as a Special Secant Class 10 Maths CBSE NCERTCircle circle theorem theorem 1 Tangent as a Special Secant Cl · of one secant segment and its external part is equal to the product of the length of the other secant segment and its external part Ex 2 Finding Segment Lengths • Find the value of x x 10 11 9 S P T R Q RP • RQ = RS • RT 9•(11 9)=10•(x 10) 180 = 10x 100 80 = 10x 8 = x SecantTangent (whole secant) • (external part) = (tangent segment)2 b c a2 If a secant

Advanced Information About Circles Geometry Circles Mathplanet

Secant Lines To Circles Ck 12 Foundation

 · Rules for Dealing with Chords, Secants, Tangents in Circles Theorem 1 If two chords intersect in a circle, the product of the lengths of the segments of one chord equal the product of the segments of the other Intersecting Chords Rule (segment piece)×(segment piece) = (segment piece)×(segment piece) Theorem Proof Theorem 2 If two secantAnd the cosecant of x is defined to be 1 divided by the sine of x cscx = 1 sinxWhen tangents intersect outside a circle, the measure of the angle they form is one half the difference of the intercepted arcs Since the tangents are at the endpoints of the same diameter, both intercepted arcs would have to measure 180 degrees This means the angle would have a measure of one half times the difference of 180 and 180, which is 0 An angle with a zero degree

Intersecting Secants Theorem Examples Solutions Worksheets Videos Games Activities

Draw A Circle And Two Lines Parallel To A Given Line Such That One Is A Tangent And The Other A Secant Brainly In

Sine, tangent, cotangent, and cosecant are odd functions while cosine and secant are even functions Ptolemy's identities, the sum and difference formulas for sine and cosine Double angle formulas for sine and cosine Note that there are three forms for the double angle formula for cosine You only need to know one, but be able to derive the other two from the PythagoreanHow to find the measure of an angle formed when a secant and a tangent intersectAs nouns the difference between secant and tangent is that secant is (geometry) a straight line that intersects a curve at two or more points while tangent is (geometry) a straight line touching a curve at a single point without crossing it there

Making Conjectures About Circles And Segments Texas Gateway

1 On The Following Graph Sketch Tangent Lines At X Chegg Com

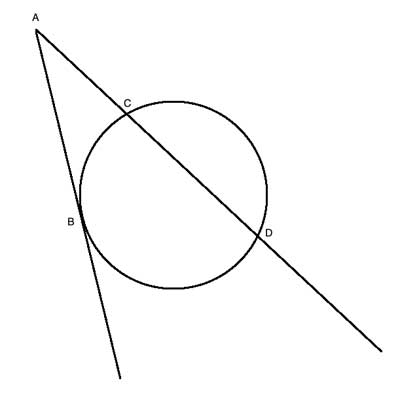
Discover more at wwwck12org http//wwwck12org/geometry/SegmentsfromSecantsandTangents/Here you'll learn how to solve for missing segments created b · Besides that, we'll use the term secant for a line segment that has one endpoint outside the circle and intersects the circle at two points Finally, we'll use the term tangent for a line that intersects the circle at just one point14 Secant and Tangent Lines 14 Secant and Tangent Lines Log InorSign Up f x = 0 3 x − 5 x 1 x 4 1 Secant Line 2 x 1

Ex 10 1 2 Fill In The Blanks Chapter 10 Class 10 Circles

Handout B Naming Tangent Secant Lines Practice Kuta Rsu 2 Math 10 Geometry

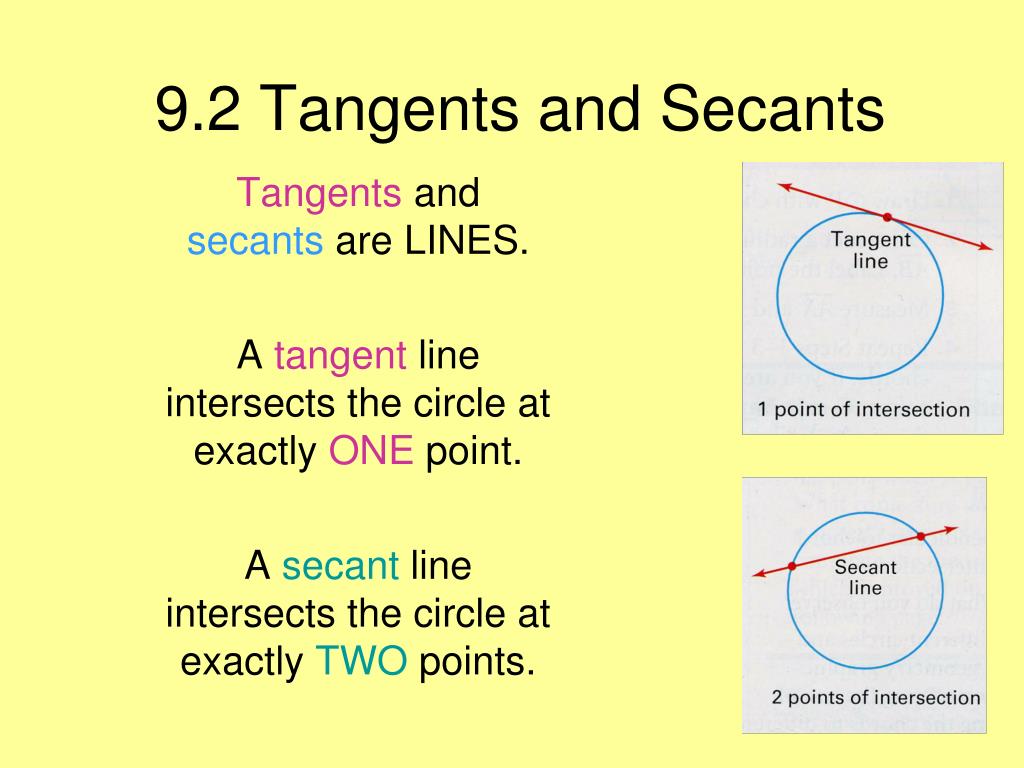
About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us CreatorsTangent line intersects circle at exactly one point Tangent, Secant Lines and Chords If a line is tangent to a circle, then it is perpendicular to the radius drawn to the point of tangency March 21, 16 Internally tangent circles Externally tangent circles Concentric circles Circles can intersect each other 0, 1, or 2 times Internal common tangent External common tangent A line orA tangent line just touches a curve at a point, matching the curve's slope there (From the Latin tangens "touching", like in the word "tangible") A secant line intersects two or more points on a curve (From the Latin secare "cut or sever") They are lines, so extend in both directions infinitely

Tangent Secant Theorem Geometry Help

Section 10 5

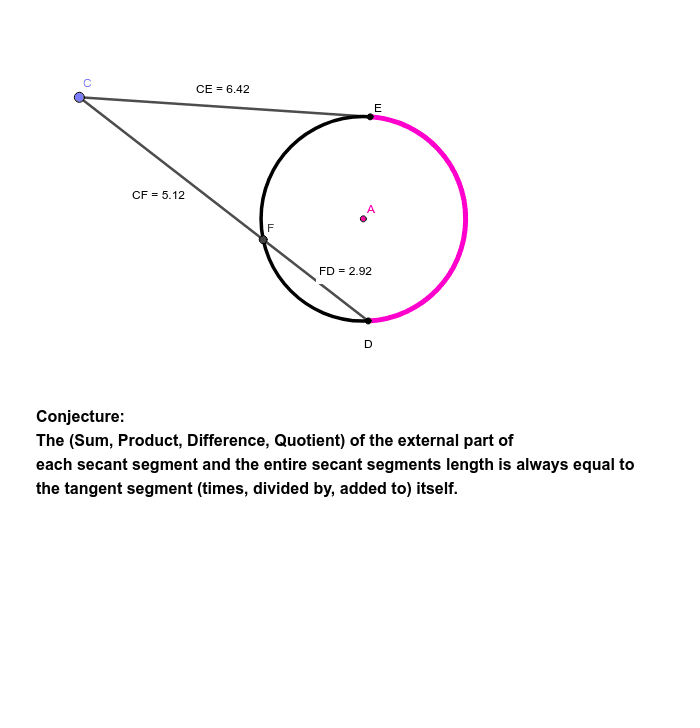
Graphing Other Trigonometric Functions SecantStacey Avant, Catherine A Eagen Investigate the relationship between the length of the external part of the secant segment (CF) and the entire secant segment (CD) and how it relates to the tangent segment (CE)What do you call a line that intersects a circle at more than one point?

In The Figure Below Vector Kl Vector Kn Mp A Gauthmath

Rules For Dealing With Chords Secants Tangents In Circles A Plus Topper

Start studying 14 tangent and secant Learn vocabulary, terms, and more with flashcards, games, and other study tools Home Subjects Create Search Log in Sign up Upgrade to remove ads Only $299/month 14 tangent and secant STUDY Flashcards Learn Write Spell Test PLAY Match Gravity Created by coletteck8 PLUS Terms in this set (9) Tangent line that touches the curve at oneFunctions are derived in some way from sine and cosine The tangent of x is defined to be its sine divided by its cosine tanx = sinx cosx The cotangent of x is defined to be the cosine of x divided by the sine of x cotx = cosx sinx The secant of x is 1 divided by the cosine of x secx = 1 cosx;Secant Tangent by Sue Lynch, NO Moore, Crystabel Riley, released 02 January 21 1 Part One 2 Part Two "Crystabel, Nathan and Sue have really done all the things that can make this music interesting they recorded their first meeting, somehow instantly created a unique group sound whilst retaining their individual identities, and were completely absorbed in 'virtuoso

Intersecting Secant And Tangent Line With Vertices On Inside Or Outside The Circle Krista King Math Online Math Tutor

Part 3 Lengths Of Segments Formed By One Tangent And One Secant Geogebra

• A chord is a line segment and both secant and tangents are straight linesIn Fig 2 (ii), XY is a secant line to the circle and A and B are called the points of intersection of the line XY and the circle with centre O 5 TANGENT AS A LIMITING CASE OF A SECANT Consider the secant XY of the circle with centre O, intersecting the circle in the points A and B Imagine that one point A, which lies on the circle, of the secant XY is fixed and the secantDay 9 – Segments of Tangents and Secants In the figure, is called a tangent secant because it is tangent to the circle at an endpoint Similarily, is a secant segment and is the external segment of The external segments are those that lie outside the circle There is a special relationship between secant segments and external secant

10 6 Secants Tangents And Angle Measures Trigonometric Functions Circle

Circlestangentchordtheorem Circle Perpendicular

 · The word tangent comes from Latin tangens meaning "touching", since the line touches the circle of unit radius, whereas secant stems fromSecant Power TheoremIf two seedlings intersect on the outside of the circle, then the product measures of one segment secant and its external segment equals the product measures of the other secant and its external semancation The Casing segment is both external and whole segment, because it is a tangent segment with one end point on theThe angle formed by the intersection of 2 tangents, 2 secants or 1 tangent and 1 secant outside the circle equals half the difference of the intercepted arcs!

Elements Of Geometry And Trigonometry 48 Geometry Scholium At A Given Point A Only One Tangent Ad Canbe Drawn To The Circumference For If Another Could Be Drawn It Would Not

Intersecting Secant And Tangent Line With Vertices On Inside Or Outside The Circle Krista King Math Online Math Tutor

 · For shifted, compressed, and/or stretched versions of the secant and cosecant functions, we can follow similar methods to those we used for tangent and cotangent That is, we locate the vertical asymptotes and also evaluate the functions for a few points (specifically the local extrema) If we want to graph only a single period, we can choose the interval for the period in more than one way The procedure for secant · The measure of an angle in the exterior of a circle formed by a tangent and a secant is equal to half the difference of the intercepted arcs The two intercepted arcs are which is 60°, and which is 110° Find half of the difference of the two arcs 1/2 × (110 C 60) = 1/ 2 × 50 = 25ºSecant lines go through two points, while tangent lines meet smoothly with the curve at one point $\hskip 2in$ $\hskip 15in$ A secant line for two points $(x_A,y_A)$ and $(x_B,y_B)$ is given by a riseoverrun formula

Intersecting Secants And Tangents With The Vertex On Inside And Outside The Circle Kristakingmath Youtube

Segments Of Secants And Tangents Ck 12 Foundation

 · This means that if the exponent on the tangent (\(m\)) is odd and we have at least one secant in the integrand we can strip out one of the tangents along with one of the secants of course The tangent will then have an even exponent and so we can use \(\eqref{eqeq4}\) to convert the rest of the tangents to secants Note that this method does require that we have at least one secantTangent, cotangent, cosecant, and secant graphs Concept Map If you already know the relationship between the equation and graph of sine and cosine functions then the other four functions can be found by identifying zeroes, asymptotes and key points Are the four new functions transformations of the sine and cosine functions?Document • Open a document • Move between pages • Grab and drag a point Tech

Circle Line Segment Theorems Geogebra

Circles Secants And Tangents

 · Tangents and secants of a circle Warm Up Write the equation of each item 1FG x = –2 2EH y = 3 32(25 –x) = x 2 4 3x 8 = 4x x = 16 x = 8 Objectives Identify tangents, secants, and chords Use properties of tangents to solve problems Vocabulary interior of a circle concentric circles exterior of a circle tangent circles chord common tangent secant tangent of a circle · Tangent can be considered as a special case of a secant line, where the two points on the curve are infinitely close (or overlap) Tangent has interesting properties and uses in mathematics What is the difference between Chord, Tangent and Secant? · About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us Creators

Tangent Lines To Circles Wikipedia

Ppt 9 2 Tangents And Secants Powerpoint Presentation Free Download Id

Some map projections contact the earth's surface along a point or line, called a tangent, while other map projections contact the earth's surface along two lines, called secants Both tangents and secants represent locations on the map projection where there is no distortionHttp//wwwmathpowerlinecom Secants and tangents of circles are formed by lines and segments The angles and segments formed have special relation

Learn Tangent Secant Theorem In 3 Minutes

Advanced Geometry Lesson 3 Circles Tangents And Secants

Properties Of Tangents By Christina Johnson

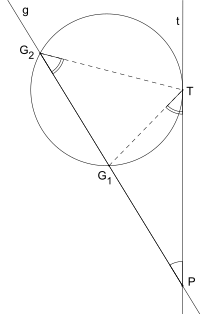
Tangent Secant Theorem Wikipedia

Intersecting Secants Theorem

Tangent Secants And Their Side Lengths From A Point Outside The Circle Theorems And Formula To Calculate Length Of Tangent Secant

Circles And Tangents Theorem Statement Proof Construction Solved Example Problems Geometry

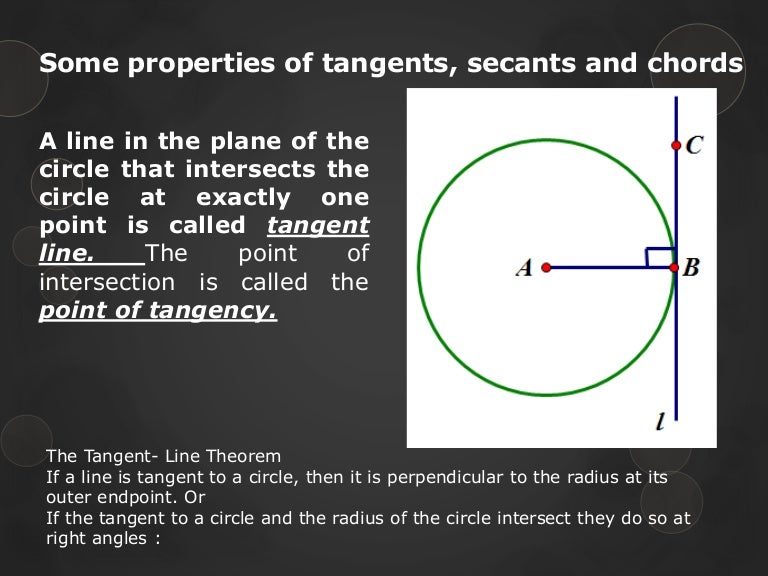
Properties Of Circle

Angle Of Intersecting Secants Theorem

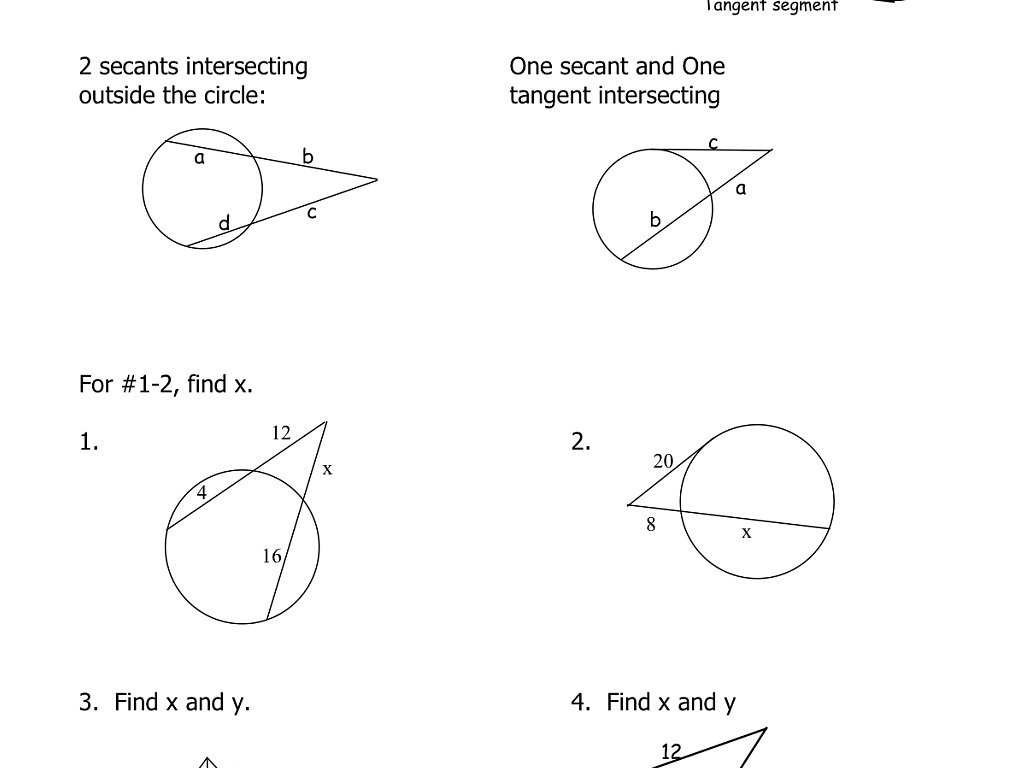
11 5 Tangents And Secants Math High School Math Geometry Models Showme

Tangent Line And Secants

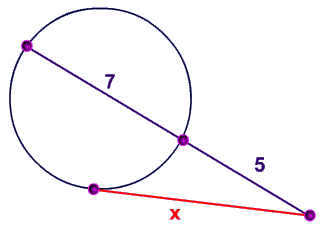
Tangent Secants And Their Side Lengths From A Point Outside The Circle Theorems And Formula To Calculate Length Of Tangent Secant

Lesson Explainer Special Segments In A Circle Nagwa

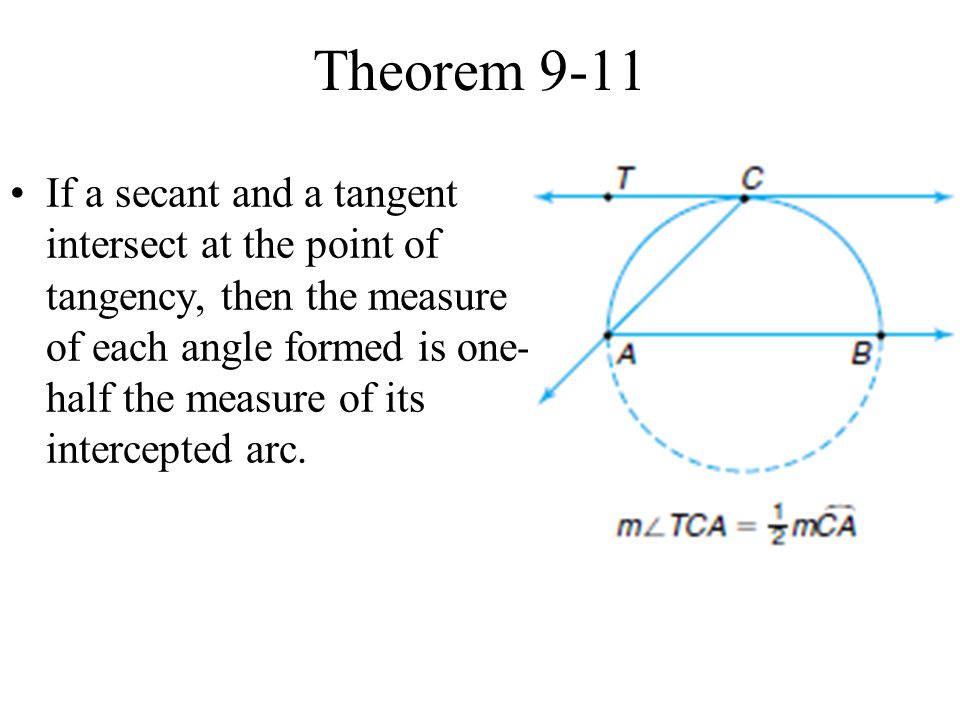
Secants Tangents And Angle Measures Ppt Video Online Download

Advanced Information About Circles Geometry Circles Mathplanet

Secants Tangents And Angle Measures Ppt Video Online Download

Tangent Secant Theorem Wikipedia

9 7 Special Segments In A Circle Geometry Mr Lee

6 Tangent Secant Theorem K12 Libretexts

Geometry 12 5a Find Measures Using Tangents And Secants 3 Theorems Youtube

Power Theorems D3 Geometry

Rules For Chords Secants Tangents Mathbitsnotebook Geo Ccss Math

Tangent Secants And Their Side Lengths From A Point Outside The Circle Theorems And Formula To Calculate Length Of Tangent Secant

Secant And Tangent Properties Of Tangents Definition Properties

Secant Tangent And Derivatives

Intersecting Secants Theorem Explained W 15 Examples

Tangent Chord Secant Rules Flashcards Quizlet

Day 9 Segments Of Tangents And Secants

Lesson Video Angles Of Intersecting Lines In A Circle Nagwa

Tangent Circles Always Have Exactly One Common Chegg Com

Kutasoftware Geometry Secant Tangent And Tangent Tangent Angles Part 1 Youtube

Segments From Secants And Tangents Read Geometry Ck 12 Foundation

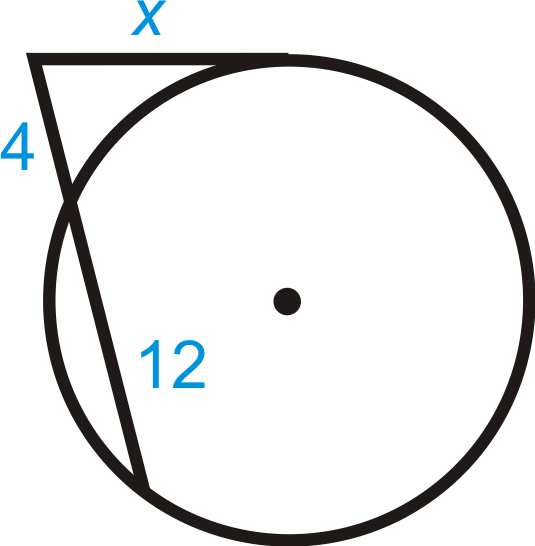
6 Tangent Secant Theorem K12 Libretexts

Circles Secants And Tangents

Tangents To Circles Section 10 1 Essential Questions

Day 7 Lines Intersecting Inside Or Outside A Circle

Circle Tangent Line From Wolfram Mathworld

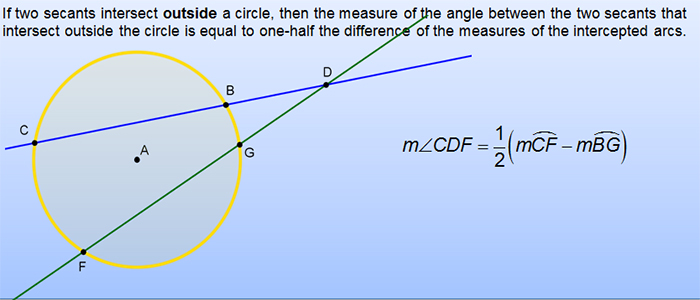
Making Conjectures About Circles And Angles Texas Gateway

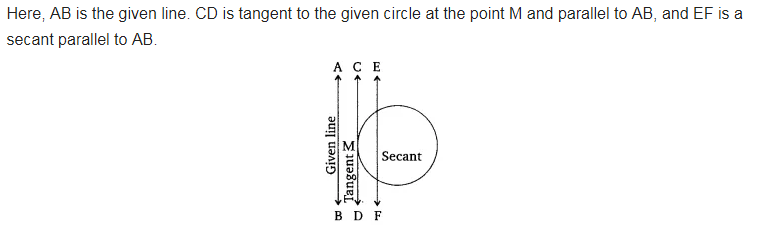
Draw A Circle And Two Lines Parallel To A Given Line Such That One Cbse Class 10 Maths Learn Cbse Forum

Ex 10 1 Q4 Draw A Circle And Two Lines Parallel To A Given Line Such That One Is A Tangent

Secant And Tangent Properties Of Tangents Definition Properties

Cbse Ncert Notes Class 10 Maths Circles

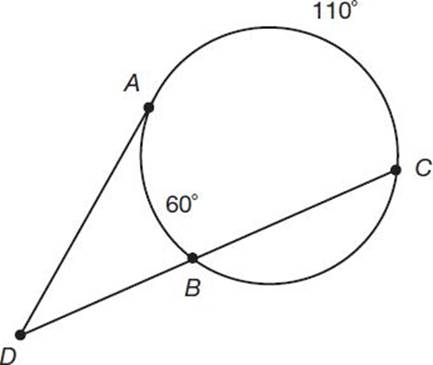
Given The Following Figure With One Tangent And One Secant Drawn To The Circle What Is The Measure Of Exam4training

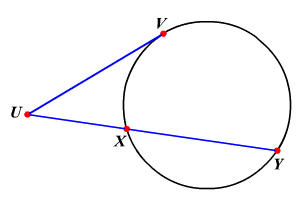
Intersecting Secant Tangent Theorem

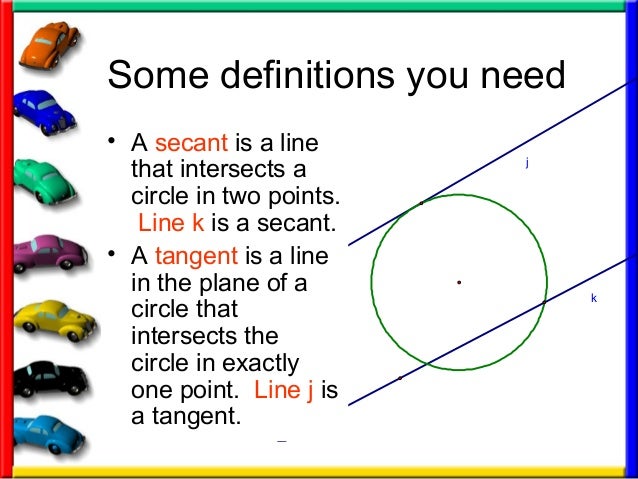
10 1 Tangents To Circles

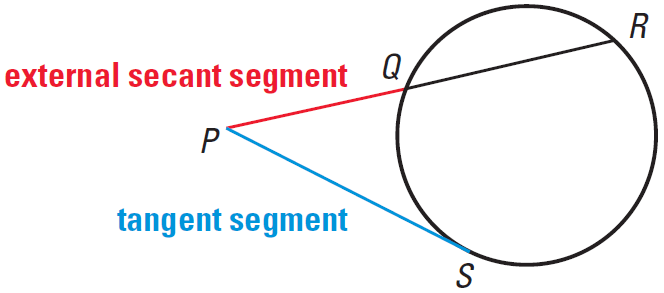
Segment Lengths In Circles

Deconstructing The Mean Value Theorem Part 3 Infinity Is Really Big

1

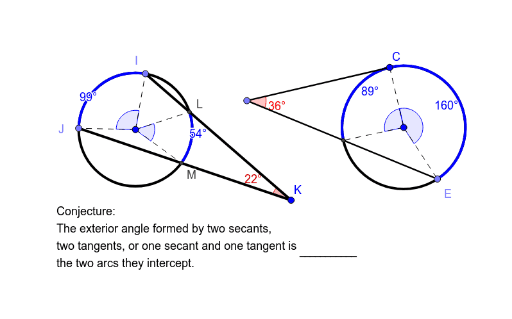
Part 2 Circle With Two Secants Or One Secant One Tangent Geogebra

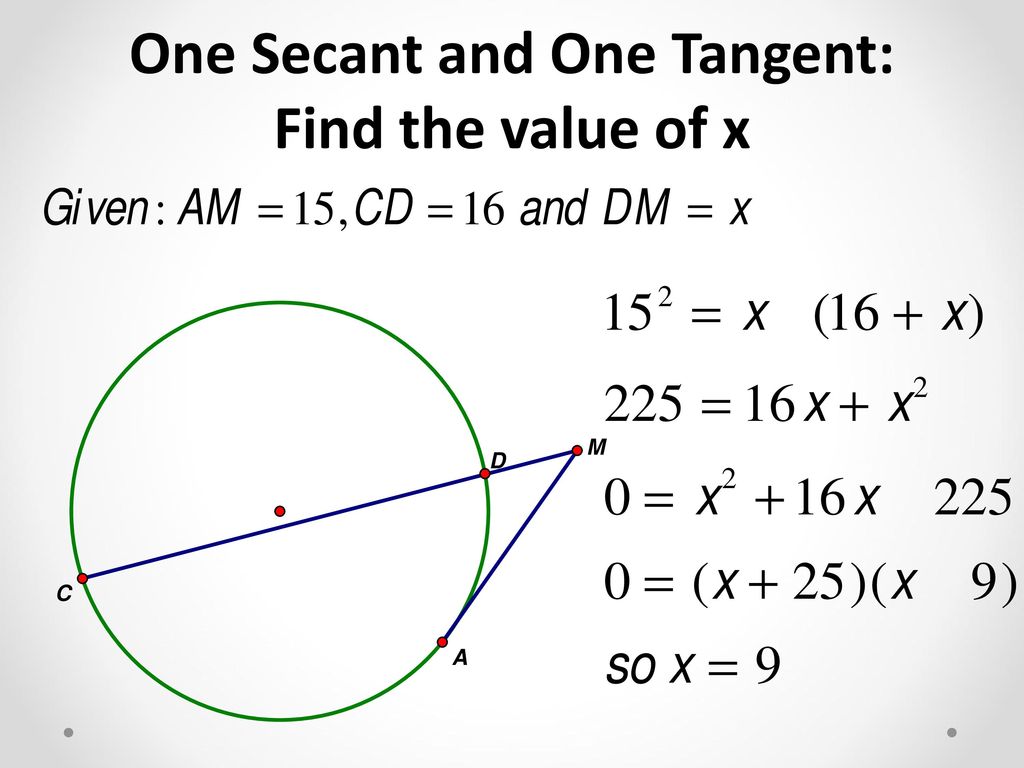
Segments Of A Circle Unit 4 Ppt Download

Circles Secants And Tangents

What Is The Difference Between Secant Tangent And Diameter Quora

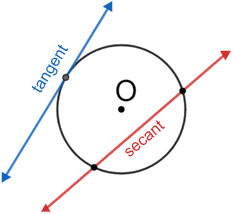
Secant

Section 11 6 Geometry Lesson Circles

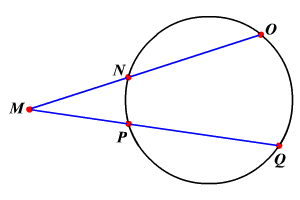
Intersecting Secants Theorem

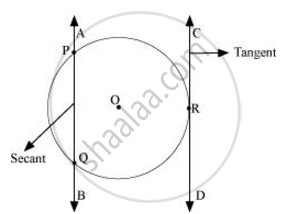
Draw A Circle And Two Lines Parallel To A Given Line Such That One Is A Tangent And The Other A Secant To The Circle Mathematics Shaalaa Com

1

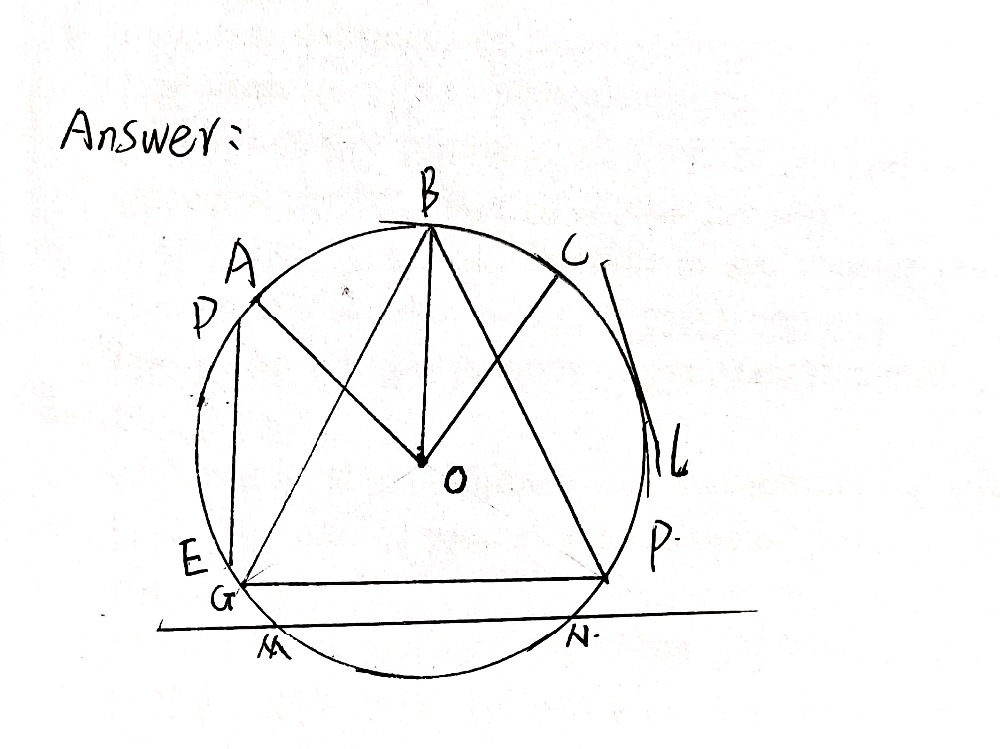
Activity 4 Using The Figure Draw And Name The Di Gauthmath

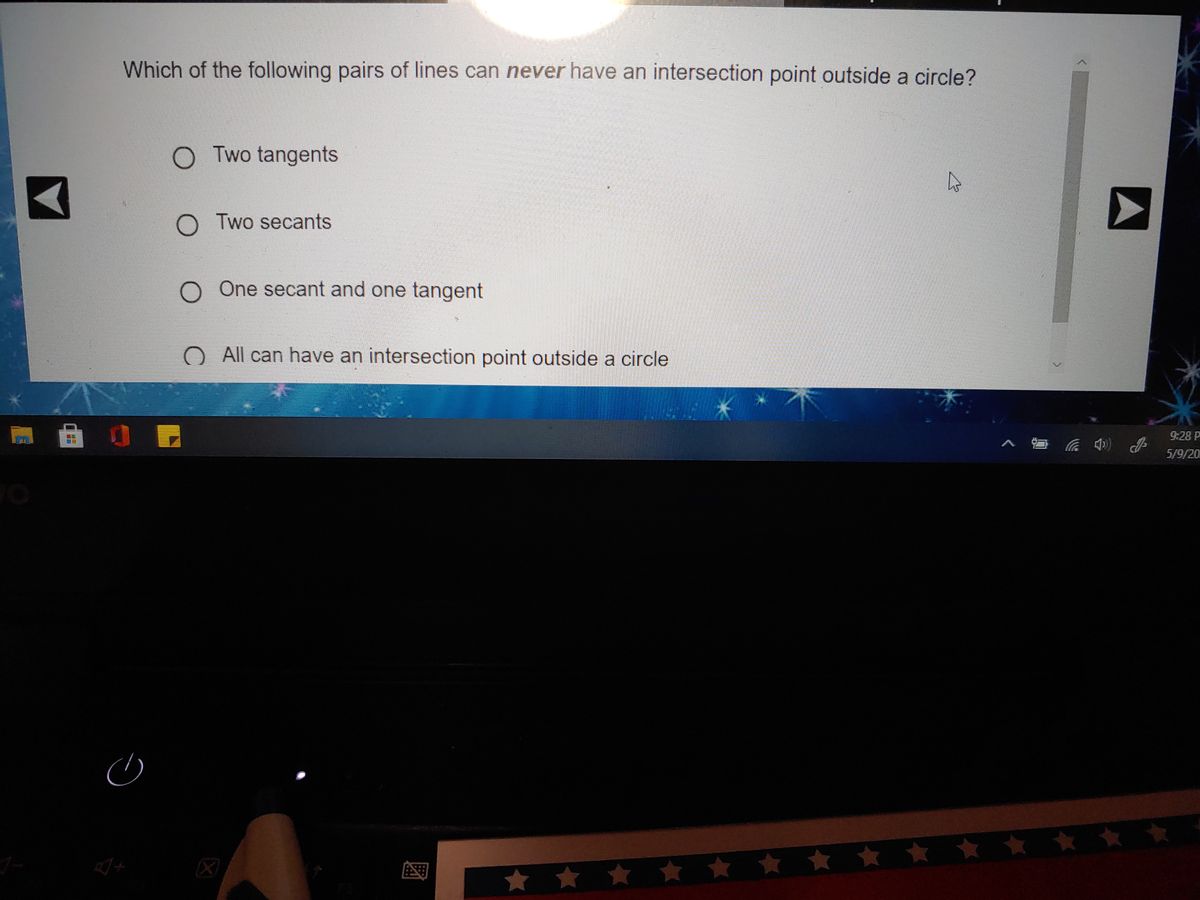
Answered Which Of The Following Pairs Of Lines Bartleby

Ex 10 1 4 Draw A Circle And Two Lines Parallel To Ex 10 1

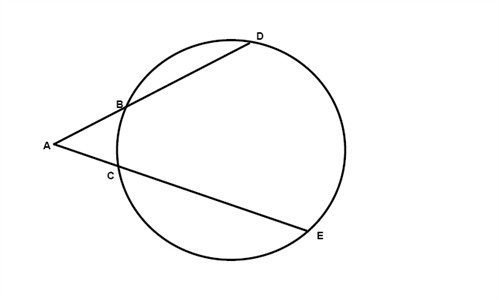
Advanced Information About Circles Geometry Circles Mathplanet

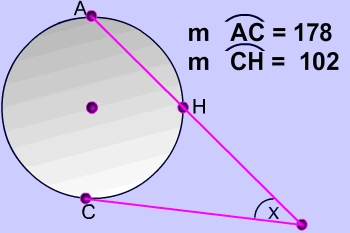
Tangent Secants Their Arcs And Angles Formula Pictures Interactive Demo And Practice Problems

Untitled Document

Day 9 Segments Of Tangents And Secants

Number Of Tangents From A Point On A Circle Geeksforgeeks

Geometry 2 Storyboard Par Cervantessc1674

Monster Circle Puzzle 2 Segments Formed By Secants Tangents And Chords Circle Math Math Geometry Teaching Geometry

Circles Tangents And Secants Shmoop

In The Following Figure A Tangent Segment Pa Touching A Circle In A And A Secant Pbc Intersects The Circle At Points C And B If Ap 13 And Bp 6 Find Pc

1

Intersecting Secants Theorem Examples Solutions Worksheets Videos Games Activities

1

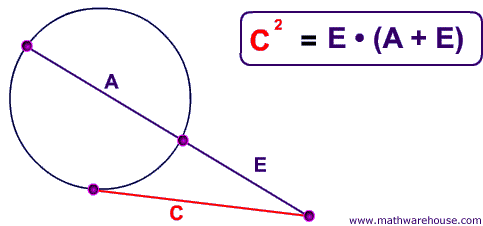
Tangent Secants And Their Side Lengths From A Point Outside The Circle Theorems And Formula To Calculate Length Of Tangent Secant

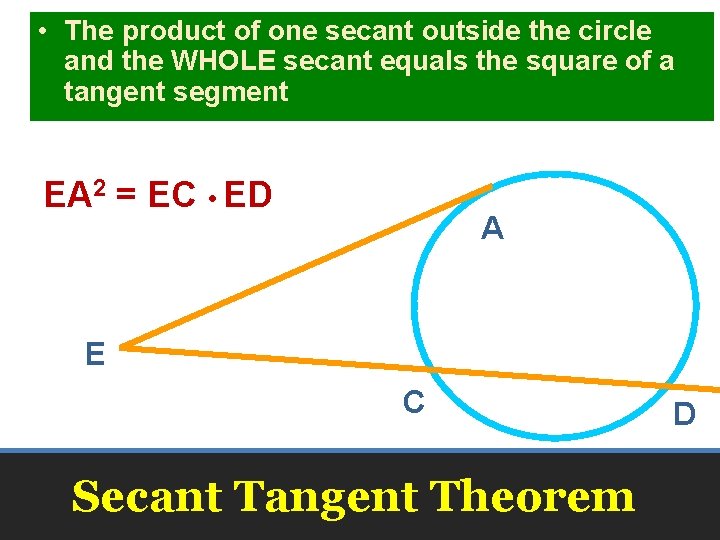
Segment Lengths Geometry 11 4 B If Two

Section 10 5

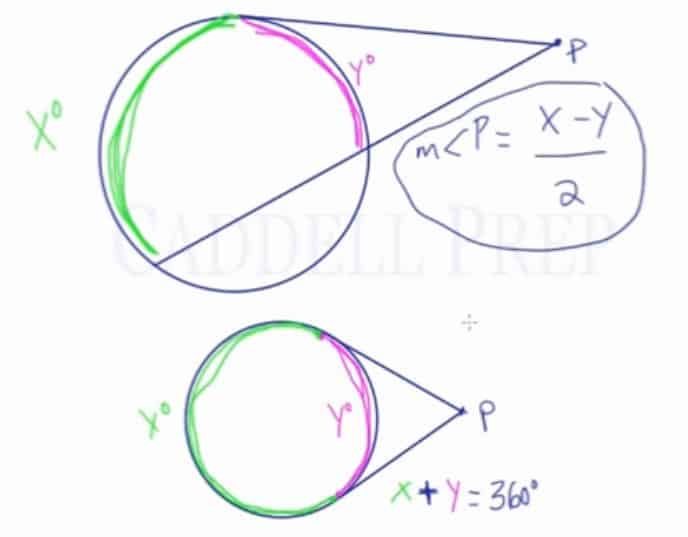
Arcs Formed By Tangents Secants Which Intersect At An External Point

Incoming Term: one secant and one tangent, one secant and one tangent calculator,